Maths
BackA-level Mathematics builds on topics in the GCSE curriculum, such as algebra and trigonometry, and also extends it into new areas such as calculus. Modules in statistics and mechanics help students begin to see practical applications of mathematics that are extremely relevant in society today.
Learning Roadmaps
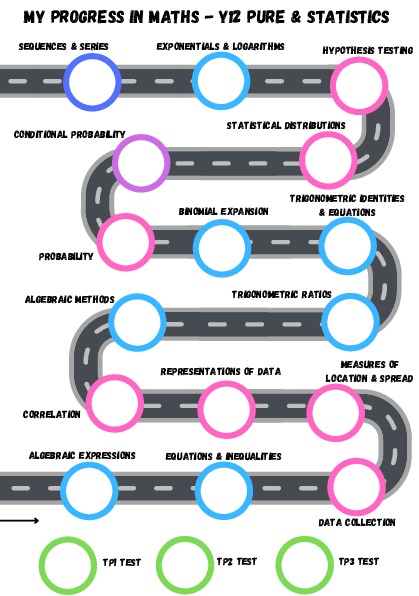
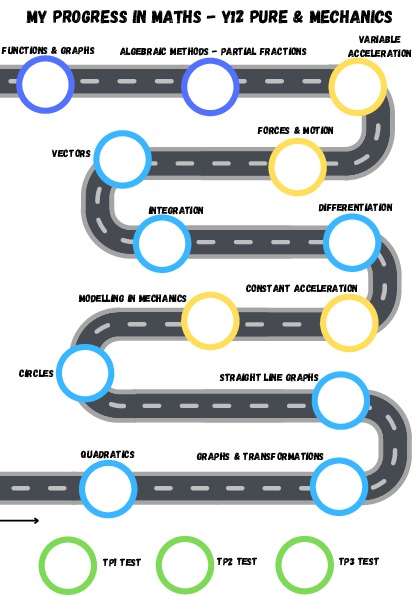
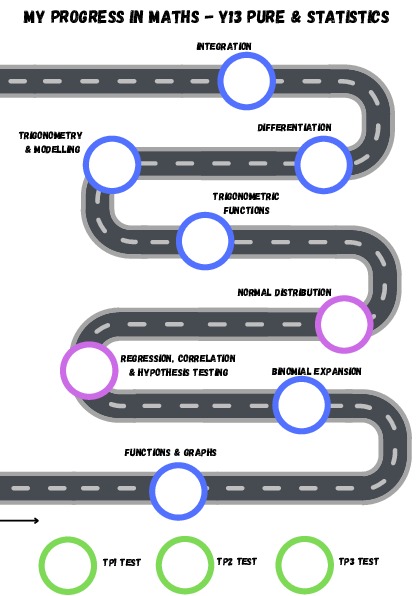
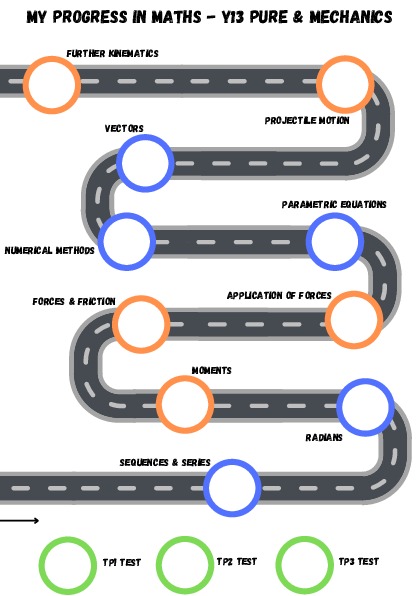
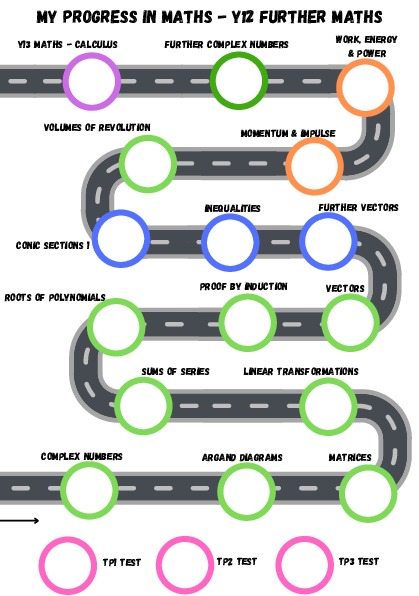
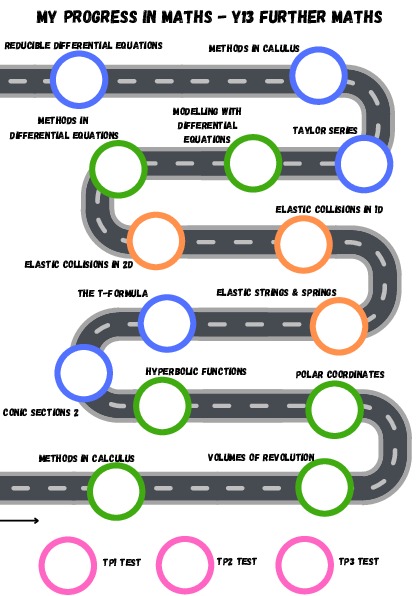

Curriculum Overview
| Year 12 | Term 1 | Term 1.5 | Term 2 |
|---|---|---|---|
| Development of topic: |
Pure Year 1 Ch1: Algebraic Expressions Ch2: Quadratics Ch3: Equations and Inequalities Ch4: Graphs & Transformations Ch5: Straight Line Graphs Ch6: Circles |
Pure Year 1 Ch7: Algebraic Methods Ch8: Binomial Expansion Ch9: Trig Ratios Ch10: Trig Identities & Ch11: Vectors Ch12: Differentiation |
Pure Year 1 Ch13: Integration Ch14: Exponentials Statistic Ch1: Data Collection Ch2: Location & Spread Mechanics Ch8: Modelling Ch9: Const Acceleration |
| Previous Knowledge Required: | Year 10 and 11 GCSE Higher Content |
Year 10 and 11 GCSE Higher Content + Half Term 1 |
Year 10 and 11 GCSE Higher Content + Half Term 1,2 |
| Skills Taught: |
Pure Year 1 Ch1: Algebraic Expressions
Ch2: Quadratics
Ch3: Equations and Inequalities
Ch4: Graphs & Transformations
Ch5: Straight Line Graphs
Ch6: Circles
|
Pure Year 1 Ch7: Algebraic Methods
Ch8: Binomial Expansion
Ch9: Trig Ratios
Ch10: Trig Identities &
Ch11: Vectors
Ch12: Differentiation
|
Pure Year 1 Ch13: Integration
Ch14: Exponentials &
Statistic Ch1: Data Collection
Ch2: Location & Spread
Mechanics Ch8: Modelling
Ch9: Const Acceleration
|
| Web Links: | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home |
| Year 12 | Term 2.5 | Term 3 | Term 3.5 |
|---|---|---|---|
| Development of topic: |
Statistics Ch3: Representing Data Ch4: Correlation
Ch5: Probability
Mechanics Ch10: Forces & Motion Ch11: Variable Accel |
Statistics Ch6: Binomial Distr. Ch7: Hypothesis Testing Pure year 2 Ch1: Algebraic Methods Ch2: Functions & Graphs |
Pure year 2 Ch3: Sequences & Series Ch4: Binomial Expansion Ch5: Radians Ch6: Trig Functions |
| Previous Knowledge Required: |
Year 10 and 11 GCSE Higher Content + Half Term 1,2,3 |
Year 10 and 11 GCSE Higher Content + Half Term 1,2,3 |
Year 10 and 11 GCSE Higher Content + Half Term 1,2,3 |
| Skills Taught: |
Statistics Ch3: Representing Data
Ch4: Correlation
Ch5: Probability
Mechanics Ch10: Forces & Motion
Ch11: Variable Accel
Const acceleration |
Statistics Ch6: Binomial Distr.
Ch7: Hypothesis Testing
*Finish Mech/Stats topics or revise using past papers
Pure year 2 Ch1: Algebraic Methods
Ch2: Functions & Graphs
|
Pure Year 1 Ch3: Sequences & Series
Ch4: Binomial Expansion
Ch5: Radians
Ch6: Trig Functions
Inverse trig functions |
| Web Links: | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home |
| Year 13 | Term 1 | Term 1.5 | Term 2 |
|---|---|---|---|
| Key Topic: |
Trigonometry Differentiation |
Integration | Statistics and Mechanics |
| Development of topic: |
Ch. 7 Trigonometry and Modelling Ch. 8 Parametric Equations Ch. 9 Differentiation |
Ch. 10 Numerical Methods Ch. 12 Vectors Ch. 11 Integration |
Stats Ch.1 Regression
Mechanics Ch. 4 Moments |
| Previous Knowledge Required: |
|
Y1 A-level Integration |
Y1 Stats and Mechanics |
| Skills Taught: |
|
|
|
| Web Links: | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home |
| Year 13 | Term 2.5 | Term 3 |
|---|---|---|
| Key Topic: | Statistics and Mechanics |
Statistics and Mechanics Revision |
| Development of topic: |
Stats Ch. 2 Conditional Probability Ch.3 Normal Distribution Mechanics Ch.5 Forces and Friction Ch.6 Projectiles Ch.7 Applications of Forces |
Mechanics Ch.8 Further Kinematics Revision and Exams |
| Previous Knowledge Required: |
Y1 Stats and Mechanics |
Y1 Mechanics |
| Skills Taught: |
|
|
| Web Links: | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home |
Further Maths
Further Maths Transition Booklet
| Year 12 - Further Maths | Term 1 | Term 1.5 | Term 2 |
|---|---|---|---|
| Key Topic: | Complex Numbers and Matrices |
Series Polynomials Proof |
Trigonometry Graph Theory |
| New Knowledge: |
Ch. 1 Complex Numbers Ch. 2 Argand Diagrams Ch. 6 Matrices Ch.7 Linear Transformations |
Ch. 3 Series Ch. 4 Roots of Polynomials Ch. 8 Proof by induction Ch. 9 Vectors Ch. 5 Volumes of Revolution |
Pure Book Y2: Ch. 6 Trigonometric Functions Ch. 7 Trigonometry and modelling Decision Maths: Ch. 3 Algorithms on Graphs Ch. 2 Graphs and Networks Ch.4 Route Inspection Ch. 1 Algorithms |
| Previous Knowledge Required: | GCSE level Trigonometry, Pythagoras, Surds |
Solving quadratic equations |
Y1 A-level trigonometry |
| Skills Taught: |
|
|
|
| Web Links: | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home |
| Year 12 - Further Maths | Term 2.5 | Term 3 | Term 3.5 |
|---|---|---|---|
| Key Topic: | Differentiation | Integration |
Complex Numbers Method of Differences |
| Development of topic: |
Pure Book Y2: Ch. 9 Differentiation Decision Maths: Ch. 6 Linear Programming Ch. 8 Critical Path Analysis |
Pure Book Y2: Ch. 11 Integration Decision Maths: Ch. 5 Travelling Salesman Ch 9. Simplex Algorithm |
Pure Y2 Book: Ensure all prerequisites for Y2 are covered Y2 Core FM Book:
Ch. 1 Complex Numbers Ch. 2 Method of Differences |
| Previous Knowledge Required: |
GCSE algebraic manipulation including indices |
Y12 A-level integration |
Y1 A-level FM Complex Numbers |
| Skills Taught: |
|
|
|
| Web Links: | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home |
| Year 13 - Further Maths | Term 1 | Term 1.5 | Term 2 |
|---|---|---|---|
| Key Topic: | Polar Coordinates |
Differential Equations |
Conic Sections |
| New Knowledge: |
Ch3. Methods in Calculus Ch.4 Volumes of Revolution Ch. 5 Polar Coordinates Ch. 6 Hyperbolics |
Ch.7 Differential Equations Ch. 8 Modelling with DEs
FP1 Ch. 1 Vectors |
Ch. 2 Conic Sections 1 Ch. 3 Conic Sections 2 Ch. 4 Inequalities Ch. 5 t-formulae Ch 6. Taylor Series |
| Previous Knowledge Required: |
Y1 FM Calculus Y1 A-level Trigonometry |
Y1 and 2 A-level calculus Y1 A-level vectors |
A-level Y1 and 2 Trigonometry Modulus function |
| New Skills: |
|
|
|
| Web Links: | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home |
| Year 13 - Further Maths | Term 2.5 | Term 3 |
|---|---|---|
| Key Topic: | Calculus |
Revision of all topics |
| Development of topic: |
Ch. 7 Methods in Calculus Ch.8 Numerical Methods Ch.9 Reducible Differential Equations |
|
| Previous Knowledge Required: |
Previous work on Differential Equations |
|
| Skills Taught: |
|
|
| Web Links: | https://sites.google.com/view/tlmaths/home | https://sites.google.com/view/tlmaths/home |

